Cara Mencari Determinan & Invers Matriks Beserta Contohnya | Matematika Kelas 11

Dalam artikel Matematika kelas 11 ini, akan menjelaskan cara mencari determinan dan invers suatu matriks disertai dengan beberapa contoh soal dan pembahasannya.
—
Di artikel sebelumnya, kita udah belajar mengenai pengertian serta operasi hitung pada matriks. Hayoo, ada yang masih ingat syarat perkalian dua matriks itu apa? Nah loh! Masa sih udah lupa aja. Coba deh baca-baca lagi artikel di link ini kalau kamu lupa.
Nah, bahasan kali ini masih seputar matriks, nih. Pasti kamu udah tau dari judul artikel di atas. Yap! Bener banget. Kita akan belajar tentang cara mencari determinan dan invers matriks. Waduh, bagaimana tuh ya? Langsung aja yuk kita simak bersama-sama.
Cara Mencari Determinan Matriks
Well, kita mulai dari cara mencari determinan matriks terlebih dahulu, ya. Kenapa? Soalnya, untuk mencari invers matriks, kita perlu mencari determinan matriksnya lebih dulu. Teman-teman ada yang udah tau apa itu determinan matriks?
Determinan adalah nilai yang dapat dihitung dari unsur-unsur suatu matriks persegi. Maksudnya matriks persegi tuh yang kayak gimana sih? Matriks persegi adalah matriks yang memiliki jumlah baris dan kolom yang sama, sehingga kalau kita gambarkan bentuk matriksnya, akan membentuk bangun layaknya persegi.
“Jadi, kalau jumlah baris dan kolomnya nggak sama, kita nggak bisa mencari determinannya?”
Jawabannya udah pasti,

(sumber: giphy.com)
Gimana, paham ya sampai sini? Oke, kita lanjut, ya. Misalnya, terdapat suatu matriks yang kita beri nama matriks A. Determinan matriks A bisa ditulis dengan tanda det (A), det A, atau |A|. Nah, cara mencari determinan suatu matriks juga berbeda-beda, tergantung dari ordonya. Kita bahas satu-satu, ya…
Baca Juga: Memahami Konsep Turunan Fungsi Aljabar
a. Determinan Matriks Ordo 2 x 2
Misalkan,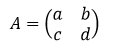 adalah matriks berordo 2 x 2. Elemen a dan d terletak pada diagonal utama, sedangkan elemen b dan c terletak pada diagonal kedua. Determinan matriks A dapat diperoleh dengan mengurangkan hasil kali elemen-elemen diagonal utama dengan hasil kali elemen-elemen diagonal kedua.
adalah matriks berordo 2 x 2. Elemen a dan d terletak pada diagonal utama, sedangkan elemen b dan c terletak pada diagonal kedua. Determinan matriks A dapat diperoleh dengan mengurangkan hasil kali elemen-elemen diagonal utama dengan hasil kali elemen-elemen diagonal kedua.

Nah, supaya kamu nggak bingung, coba kita perhatikan contoh soal di bawah ini.
Contoh soal mencari determinan matriks 2 x 2
Tentukanlah determinan matriks berikut!
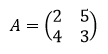
Pembahasan:
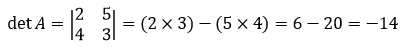
Teman-teman, mudah kan ternyata. Hm, kira-kira, mencari determinan matriks berordo 3×3 mudah juga nggak ya? Yuk, kita cari tau!
b. Determinan Matriks Ordo 3 x 3
Misalkan,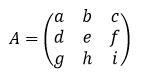 adalah matriks berordo 3 x 3. Terdapat dua cara yang bisa dilakukan untuk mencari determinannya, yaitu menggunakan aturan Sarrus dan metode minor-kofaktor.
adalah matriks berordo 3 x 3. Terdapat dua cara yang bisa dilakukan untuk mencari determinannya, yaitu menggunakan aturan Sarrus dan metode minor-kofaktor.

Hmm… Kamu pasti bingung ya maksud rumus di atas. Tenang aja, di bawah ini udah ada contoh soal dan pembahasannya kok. Jadi, bisa kamu pahami dengan baik. Tapi, jangan cuma dibaca aja ya. Supaya kamu lebih mudah paham, coba deh ikutan corat-coret di kertas. Yuk, siapkan pulpen dan kertasnya!
Baca Juga: Kedudukan Titik dan Garis Lurus pada Lingkaran
Contoh soal mencari determinan matriks 3 x 3
Tentukan determinan matriks berikut ini menggunakan aturan Sarrus dan metode minor-kofaktor!
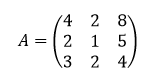
Pembahasan:
-
Aturan Sarrus
Agar lebih mudah, kita tulis kembali elemen-elemen pada kolom ke-1 dan ke-2 di sebelah kanan matriks A sebagai berikut:
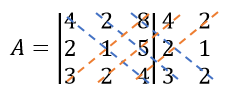
Kemudian, kita tarik garis putus-putus seperti gambar di atas. Kalikan elemen-elemen yang terkena garis putus-putus tersebut. Hasil kali elemen yang terkena garis putus-putus berwarna biru diberi tanda positif (+), sedangkan hasil kali elemen yang terkena garis putus-putus berwarna oranye diberi tanda negatif (-). Ingat urutan penulisannya juga, ya!
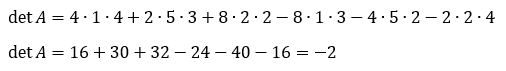
Sepintas terlihat cukup rumit ya. Tapi, kalau kamu sering berlatih soal, pasti akan hafal dengan sendirinya. Jadi, jangan malas untuk berlatih soal, ya! Sekarang, kita coba kerjakan menggunakan metode yang satunya lagi kuy!
-
Metode Minor-Kofaktor
Berdasarkan rumus minor-kofaktor di atas, determinan matriks A dapat dicari dengan menghitung jumlah seluruh hasil kali antara kofaktor matriks bagian dari matriks A dengan elemen-elemen pada salah satu baris atau kolom matriks A. Jadi, pertama, kita pilih salah satu baris atau kolom matriks A untuk mendapatkan nilai determinannya. Misalnya, kita pilih baris ke-1. Elemen-elemen matriks baris ke-1, yaitu a11, a12, dan a13.
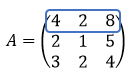
Selanjutnya, karena kita pilih elemen-elemen pada baris ke-1, rumus determinan matriks yang kita gunakan adalah sebagai berikut:
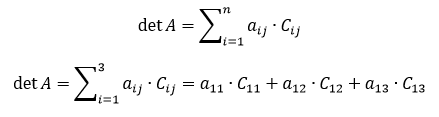
Langkah kedua, kita cari kofaktor matriks bagian dari matriks A (Cij). Cij = (-1)i+j Mij dan Mij = det Aij dengan Aij merupakan matriks bagian dari matriks A yang diperoleh dengan menghilangkan baris ke-i dan kolom ke-j. Maksudnya bagaimana? Oke, coba kamu perhatikan baik-baik ya.
Sebelumnya, kita telah memilih elemen-elemen pada baris ke-1, yaitu a11, a12, dan a13. Oleh karena itu, matriks bagian dari matriks A nya adalah A11, A12, dan A13.
- A11 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-1.
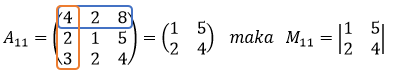
- A12 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-2.
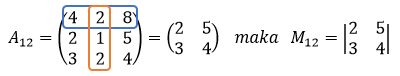
- A13 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-3.
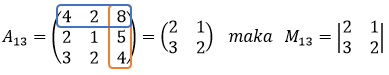
Sehingga,
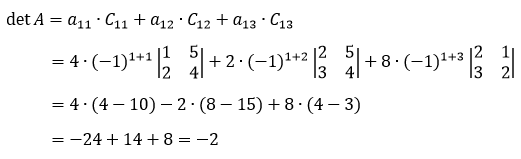
Kalau kamu perhatikan, nilai determinan matriks A yang dihasilkan menggunakan dua metode di atas akan sama aja ya. Jadi, kamu tinggal pilih nih, mana metode yang menurutmu paling mudah. Tapi, meskipun begitu, ada baiknya kamu juga pahami kedua-duanya. Kenapa? Siapa tau di ujian nanti keluar dua-duanya, loh.
—
Mau punya banyak latihan soal? Langsung aja cek fitur Bank Soal di aplikasi Ruangguru ya.
Oh iya, kamu juga perlu tau nih, determinan matriks memiliki beberapa sifat sebagai berikut:

Teman-teman, ada pertanyaan nggak sejauh ini? Kalau ada yang ingin ditanyakan, tulis aja pertanyaanmu di kolom komentar, ya. Kita lanjut ke materi berikutnya yuk, yaitu invers matriks. Ada yang udah nggak sabar mau tau cara mencari invers suatu matriks? Yok lah kita simak bahasan berikut.
Cara Mencari Invers Matriks
Kamu pasti nggak asing lagi dengan istilah invers. Saat mendengar kata invers, kamu pasti teringat materi fungsi invers yang udah pernah kamu pelajari sebelumnya.
Invers dapat juga diartikan sebagai lawan dari sesuatu (kebalikan). Invers matriks adalah kebalikan (invers) dari sebuah matriks. Jadi, apabila matriks tersebut dikalikan dengan inversnya, maka akan menjadi matriks identitas.
Pada fungsi invers, kita disuruh mencari kebalikan dari fungsi tersebut. Misalnya aja, invers dari f(x) = 2x, maka jawabannya adalah f-1 (x) = ½ x. Gimana cara mencarinya? Kalau lupa, bisa langsung klik link di bawah ini.
Baca Juga: Apakah Fungsi Invers itu?
Invers pada fungsi dengan invers pada matriks tentu aja berbeda. Selain itu, sama halnya dengan determinan, ordo matriks mempengaruhi cara mencari invers pada matriks tersebut.
Nah, jika suatu matriks memiliki invers, maka dapat dikatakan matriks tersebut adalah matriks nonsingular. Sebaliknya, jika suatu matriks tidak memiliki invers, maka matriks tersebut merupakan matriks singular.
Teman-teman, untuk penjelasan lebih lengkapnya mengenai mencari invers matriks dapat kamu perhatikan penjelasan di bawah ini.
a. Invers Matriks Ordo 2 x 2

Kita langsung ke contoh soal ya agar kamu semakin paham.
Contoh soal mencari invers matriks ordo 2 x 2
Tentukanlah invers dari matriks berikut.
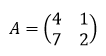
Pembahasan:
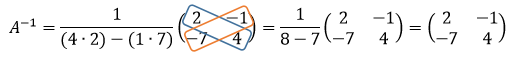
Catatan: elemen-elemen yang berada di lingkar biru merupakan diagonal utama matriks A yang ditukar posisinya, sedangkan elemen-elemen yang berada di lingkar oranye merupakan diagonal kedua matriks A yang dikalikan dengan minus satu (-1).
Gimana, paham ya dengan pembahasan di atas. Lanjut ke invers matriks ordo 3 x 3 yuk!
b. Invers Matriks Ordo 3 x 3
Mencari invers matriks berordo 3 x 3 dapat dilakukan dengan dua cara, yaitu dengan adjoin dan transformasi baris elementer. Hm, kira-kira seperti apa ya penjelasan lebih detailnya. Mari kita bahas satu persatu, ya.
-
Invers matriks ordo 3 x 3 dengan adjoin
Pada penjelasan sebelumnya tentang determinan matriks, kamu udah tau kan bagaimana cara mencari kofaktor dari suatu matriks. Nah, dari kofaktor-kofaktor tersebut, kita dapat menentukan adjoin matriksnya, lho. Adjoin matriks merupakan transpose dari suatu matriks yang elemen-elemennya merupakan kofaktor dari elemen-elemen matriks tersebut.

Sekarang, coba perhatikan contoh soal di bawah ini.
Contoh soal mencari invers matriks ordo 3 x 3 dengan adjoin
Tentukan invers matriks berikut dengan menggunakan adjoin!
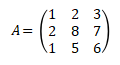
Penyelesaian:
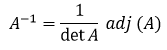
Oke, berdasarkan rumus di atas, kita membutuhkan determinan dan adjoin matriks A. Pertama, kita cari terlebih dahulu determinan matriks A menggunakan metode yang sudah dijelaskan sebelumnya. Bisa dengan cara aturan Sarrus ataupun metode minor-kofaktor. Misalnya, kita akan menggunakan metode Sarrus, sehingga:
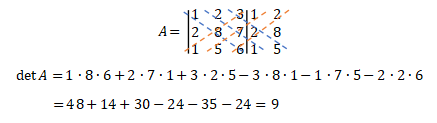
Kemudian, kita tentukan adjoin matriks dengan mencari kofaktor matriks A tersebut.
.png)
Oleh karena itu,
.png)
Jadi,
.png)
-
Invers matriks ordo 3 x 3 dengan transformasi baris elementer
Untuk menentukan invers matriks menggunakan transformasi baris elementer, kamu dapat mengikuti langkah-langkah berikut ini.

Bingung ya sama langkah-langkah di atas? Yaudah, supaya nggak bingung, di bawah ini ada contoh soal, nih. Gimana kalo kita kerjakan sama-sama. Pulpen dan kertas tadi masih ada, kan?
Contoh soal mencari invers matriks 3 x 3 dengan transformasi baris elementer
Tentukan invers matriks A dengan transformasi baris elementer.
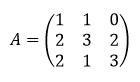
Pembahasan:
Pertama-tama, kita bentuk matriks A menjadi matriks (A3|I3).
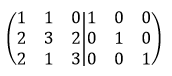
Lalu, kita transformasikan matriks (A3|I3) ke bentuk (I3|A3). Kita bisa menggunakan beberapa cara seperti yang dijelaskan poin a-d pada langkah ke-2 rumus di atas.
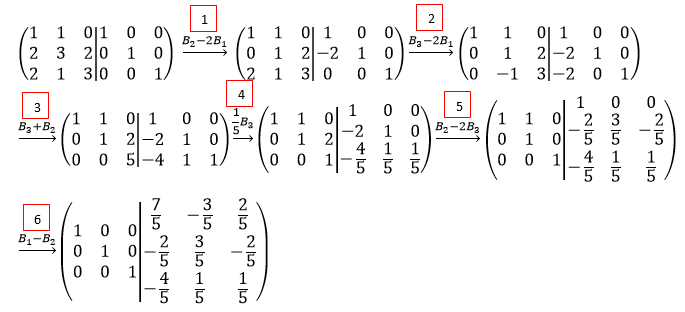
Keterangan:
1) B2-2B1 = elemen-elemen baris ke-2 dikurang 2 kali elemen-elemen baris ke-1.
2) B3-2B1 = elemen-elemen baris ke-3 dikurang 2 kali elemen-elemen baris ke-1.
3) B3+B2 = elemen-elemen baris ke-3 ditambah elemen-elemen baris ke-2.
4) 1/5B3 = elemen-elemen baris ke-3 dikali degan ⅕.
5) B2-2B3 = elemen-elemen baris ke-2 dikurang 2 kali elemen-elemen baris ke-3.
6) B1-B2 = elemen-elemen baris ke-1 dikurang elemen-elemen baris ke-2.
Sehingga, diperoleh invers matriks A, yaitu:
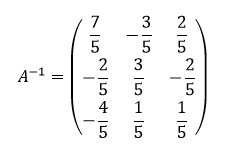

“Ingin berkata kasar tapi diriku terlalu Masya Allah”.
Pusing ya? Belajarnya pelan-pelan aja dulu. Baca dan pahami penjelasannya berulang-ulang. Selain itu, coba juga untuk latihan mengerjakan beberapa soal. Ingat! Belajar Matematika itu butuh kesabaran, waktu, dan ketekunan, loh.
Makanya, jangan harap sekali belajar langsung hafal rumus dan expert menjawab soal. Apalagi kalau besok ada ulangan, terus baru hari ini kamu belajar. Duh! Hasilnya udah pasti kurang maksimal.
Coba deh baca artikel 7 solusi belajar menghadapi ulangan Matematika di blog Ruangguru biar lain kali kamu punya strategi yang tepat agar ulangan kamu nggak remed terus.
Nah, teman-teman, kita lanjut ya. Invers pada matriks juga memiliki beberapa sifat yang bisa kamu ketahui. Apa aja ya? Ini dia!

Waduh, banyak juga ya materi yang kita pelajari hari ini. Semoga penjelasan mengenai cara mencari determinan dan invers matriks di atas tadi bermanfaat ya buat kamu.
Oh iya, kalau misalnya kamu masih kurang mengerti dengan materi ini dan ingin penjelasan yang lebih lengkap dan menarik, kamu bisa kok cobain belajar lewat aplikasi ruangbelajar. Bukan hanya video animasi menariknya aja yang bikin kamu nggak gampang bosen, tapi juga Master Teachernya yang asik dan keren-keren. Buruan langganan yuk sekarang!
Referensi:
Wirodikromo, S. dan Darmanto, M. (2019) Matematika untuk SMA/MA Kelas XI kelompok Wajib 2. Jakarta:Erlangga.
Artikel ini telah diperbaharui pada 27 Februari 2024.















