4 Metode Pembuktian Matematika | Matematika Kelas 11

Kamu sudah tahu belum kalau ada 4 metode pembuktian dalam matematika, yaitu pembuktian langsung, kontraposisi, kontradiksi, dan induksi matematika. Yuk, kita pelajari!
—
Albert Einstein, seorang fisikawan terkemuka, pernah lho mempertanyakan, kenapa ya teori matematika yang padahal hanya berasal dari pikiran manusia semata, bukan dari pengalaman, bisa sangat sesuai dan berlaku untuk benda-benda di dunia nyata? Kalau kita ambil contoh, fisika misalnya, ilmu ini bisa diterima semua orang karena pembuktiannya disaksikan lewat eksperimen. Kalau matematika? Nah, sebenarnya teori matematika juga selalu bisa dibuktikan dan sesuai dengan logika.
Logika dalam matematika? Pembuktian? Gimana tuh maksudnya? Logika dalam matematika bisa diingat kembali materinya pada artikel tentang logika matematika. Kalau pembuktian, ada beberapa cara untuk membuktikan dalam matematika, yaitu pembuktian langsung, kontraposisi, kontradiksi, dan induksi matematika. Kita cek satu-satu di artikel berikut ini, ya!
1. Pembuktian Langsung
Pembuktian langsung adalah metode pembuktian yang menggunakan alur maju. Mulai dari pendefinisian sampai menghasilkan kesimpulan. Gampangnya sih, “kalau A maka B dan kalau B maka C”. Nah, untuk menggunakan alur maju, maka pernyataan-pernyataan sebelumnya harus benar. Supaya nggak bingung, kita langsung coba buktikan pernyataan ini.
“Jumlah dari dua bilangan genap adalah bilangan genap”
Ya… kalau kita pikir-pikir, pasti sih, 2 + 2 = 4 dan 4 + 10 = 14. Tapi, gimana ya buat bisa membuktikan kalau pernyataan itu berlaku buat semua bilangan genap? Pembuktiannya begini:
Jadi, pertama kamu definisikan dulu tuh bilangan genap itu seperti apa. Misalnya, ada bilangan genap sembarang m dan n. Dari definisi bilangan genap, m dan n dapat ditulis:
m = 2k, dengan k adalah suatu bilangan bulat.
n = 2i, dengan i adalah suatu bilangan bulat.
Bila definisinya sudah benar, kita ke pernyataan selanjutnya. Karena kita ingin membuktikan jumlah dua bilangan genap, maka berdasarkan definisi di atas, jumlah dua bilangan genap bisa kita jabarkan seperti ini:
m + n = 2k + 2i
Kemudian, kamu juga butuh sedikit memanipulasi penjumlahan itu agar bisa mendapat bentuk yang diinginkan. m + n = 2k + 2i bisa kita ubah menjadi 2 (k + i), dengan (k + i) juga bilangan bulat.
m + n = 2k + 2i = 2 (k + i), dengan (k + i) bilangan bulat.
Setelah itu, lanjut deh ke kesimpulan. Ingat lho, kesimpulannya harus berdasarkan pernyataan sebelumnya. m + n dapat ditulis menjadi 2 kali suatu bilangan bulat (k + i). Sesuai definisi bilangan genap, maka m + n merupakan bilangan genap juga. Apakah pembuktian ini berlaku untuk seluruh bilangan genap? Iya, karena di awal sudah disebutkan kalau m dan n adalah bilangan genap sembarang. Jadi, terbukti, ya.
Baca juga: Rumus Bunga Majemuk dan Cara Menghitungnya
2. Kontraposisi
Kontraposisi adalah salah satu metode pembuktian tidak langsung. Kontraposisi memanfaatkan prinsip logika matematika, yaitu:
p → q ≡ ∼q → ∼p
Artinya, kalau mau membuktikan pernyataan p akan menghasilkan pernyataan q itu benar, maka buktikan aja pernyataan bukan q maka menghasilkan bukan p. Bingung, ya? Nah, untuk memahami lebih lanjut, coba deh buktikan:
“Bila n bilangan bulat dan 7n + 9 bilangan genap, maka n bilangan ganjil”
Gimana nih membuktikannya pakai kontraposisi? Misalnya, pernyataan p adalah 7n + 9 bilangan genap, dan pernyataan q adalah n bilangan ganjil. Maka, yang kita buktikan adalah bila n bukan bilangan ganjil (bilangan genap), maka 7n + 9 bukan bilangan genap (bilangan ganjil). Jadi, negasi dari kebalikannya, ya. Penyelesaian lebih lanjutnya begini:
Misalkan ada bilangan genap sembarang n. Dari definisi bilangan genap, n dapat dinyatakan sebagai berikut:
n = 2k, dengan k bilangan bulat.
Selanjutnya, karena n = 2k, maka 7n + 9 bisa dituliskan menjadi 7n + 9 = 7(2k) + 9 atau 2 (7k) + 9.
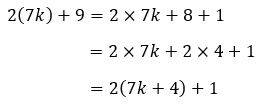
Nah, 7k + 4 sudah pasti merupakan bilangan bulat juga karena di awal, kita memisalkan k adalah bilangan bulat. 7k + 4 bisa dimisalkan dengan m, sehingga:
2(7k) + 9 = 2m + 1, dengan m bilangan bulat.
Sesuai definisi bilangan ganjil, maka 2(7k) + 9 atau 7n + 9 adalah bilangan ganjil. Terbukti kan bila n bukan bilangan ganjil, maka 7n + 9 juga bukan bilangan genap. Secara nggak langsung, dapat disimpulkan deh bila n bilangan bulat dan 7n + 9 bilangan genap maka n bilangan ganjil, hehehe…
3. Kontradiksi
Kontradiksi ini juga termasuk pembuktian tidak langsung. Kita memanfaatkan prinsip logika matematika, yaitu:
Jika p → q bernilai benar padahal q salah, maka p salah
Hmm gimana tuh maksudnya? Coba deh kita buktikan pernyataan ini dengan kontradiksi.
“Bila n bilangan bulat dan n bilangan genap, maka 7n + 9 bilangan ganjil”
Nah, kita misalkan dulu pernyataan p adalah n bilangan genap dan pernyataan q adalah 7n + 9 adalah bilangan ganjil. Maka, dengan kontradiksi, kita buktikan pernyataan n bukan bilangan genap (bilangan ganjil), maka untuk 7n + 9 adalah bilangan ganjil benar akan muncul suatu kontradiksi. Coba deh perhatikan penyelesaiannya di bawah ini:
Misalkan ada bilangan ganjil sembarang n. Dari definisi bilangan ganjil, n dapat dinyatakan sebagai berikut:
n = 2k + 1, dengan k bilangan bulat.
Karena n = 2k + 1, maka 7n + 9 dapat dituliskan menjadi:
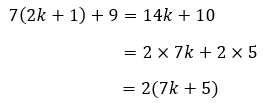
7k + 5 pastinya merupakan bilangan bulat juga karena k adalah bilangan bulat. Kita bisa misalkan 7k + 5 dengan m, sehingga:
7n + 9 = 14k + 10 = 2m
Nah, 14k + 10 atau 7n + 9 dapat dinyatakan dalam 2 kali suatu bilangan bulat. Padahal, itu merupakan definisi bilangan genap. Berarti, kontradiksi dengan asumsi awal yang menyatakan 7n + 9 adalah bilangan ganjil. Itu artinya, asumsi awal n adalah bilangan ganjil, salah.
Baca juga: Konsep Limit Fungsi Aljabar dan Sifat-Sifatnya
Lihat kan, ternyata ada kontradiksi bila n adalah bilangan ganjil? Maka, secara tidak langsung, pernyataan “bila n bilangan genap, maka 7n + 9 bilangan ganjil” benar.
4. Induksi Matematika
Induksi matematika digunakan untuk membuktikan suatu pernyataan untuk setiap bilangan asli. Untuk melakukan pembuktian menggunakan induksi matematika, ada langkah-langkahnya, nih. Bagaimana langkah-langkah melakukan induksi matematika?

Waduh, maksudnya apa tuh ya langkah-langkah di atas. Oke, biar nggak bingung, mending langsung aja kita aplikasikan ke contoh soal di bawah ini.
Buktikan deret 1 + 2 + 3 + … + n = 1/2 n(n+1)
- Langkah pertama
Kita akan buktikan untuk n = 1 adalah benar. Karena pernyataan tersebut merupakan deret, maka n di sini maksudnya jumlah suku pertama deret tersebut. Nah, yang diminta n = 1, berarti jumlah suku pertamanya hanyalah 1. Kemudian, kita substitusi semua n dengan 1. Jadi,
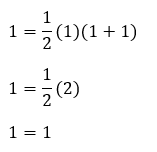
Langkah pertama terbukti ya karena ruas kiri dan kanannya sama.
- Langkah kedua
Kita asumsikan pernyataan benar untuk n = k. Berarti jumlah suku pertamanya itu dari 1 + 2 + 3 + … + k, ya. Sehingga,
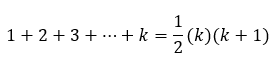
Pernyataan tersebut kita asumsikan atau kita anggap benar. Kemudian, kita lanjut ke langkah ketiga.
- Langkah ketiga
Buktikan untuk pernyataan n = k + 1 juga benar. Kita bisa membuktikannya menggunakan modal dari langkah kedua. Karena kita mau n = k + 1, maka di ruas kiri, kita tambahkan satu suku, yaitu k + 1. Jadi,
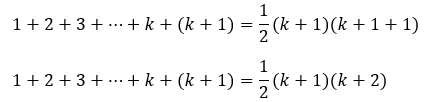
Di langkah kedua, kita peroleh 1 + 2 + 3 + … + k = 1/2 (k)(k + 1). Maka,
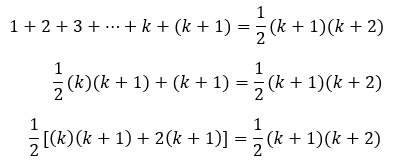
Selanjutnya, kamu ingat nggak dengan sifat distribusi pada perkalian? Kalau ada (a + b)(c + d), maka bisa menjadi a(c + d) + b(c + d). Nah, di ruas kiri, bisa kita ubah persamaannya menggunakan sifat perkalian distribusi.
Misalnya, a = k, b = 2, dan (c + d) = (k + 1). Berarti,
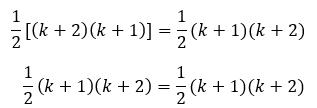
Karena ruas kiri dan kanannya sudah sama, berarti terbukti kalau untuk deret 1 + 2 + 3 + … + n nilainya sama dengan 1/2 n(n + 1).
Baca juga: Mengulik Materi Logika Matematika Konvers, Invers, dan Kontraposisi

Oke, selesai sudah pembahasan kali ini. Wah, sekarang kamu sudah tau ya empat metode pembuktian dalam matematika. Ada pembuktian langsung, kontraposisi, kontradiksi, dan induksi matematika. Semuanya sudah dibahas lengkap di artikel ini disertai dengan contoh pembahasannya.
Gimana, asik kan ternyata belajar pembuktian matematika? Masih buanyaak loh yang bisa dipelajari tentang materi ini. Nah, kalau kamu butuh tambahan video animasi dan pembahasan soal agar belajarmu jadi lebih mudah dan menyenangkan, daftar aja di ruangbelajar. Sekarang, ruangbelajar sudah dilengkapi fitur-fitur baru, seperti playlist belajar salah satunya. Tuh, kan semakin mendukung pembelajaran kamu aja, nih. So, langsung sikat!
Referensi:
Wirodikromo, S. dan Darmanto, M. (2019). Matematika untuk SMA/MA Kelas XI kelompok Wajib 2. Jakarta: Erlangga.
Artikel ini telah diperbarui pada 22 Juni 2022.












