Latihan Soal Tryout UTBK 1 Tahun 2021: Matematika IPS

Ingin UTBK 2021 kamu mendapatkan hasil maksimal? Yuk, persiapkan dirimu mulai sekarang dengan mempelajari latihan soal tryout UTBK Episode 1 tahun 2021 untuk mata pelajaran Matematika IPS.
—
Sudahkah kamu mengikuti try out UTBK 1 dari ruanguji? Jika penasaran mengenai seperti apa pembahasan soal-soalnya, simak artikel ini ya. Berikut merupakan kumpulan latihan soal tryout UTBK 1 tahun 2021 untuk mata pelajaran Matematika IPS yang bisa kamu pelajari. Semoga membantu!

1. Jika log (2x + 8y)= 2 dan 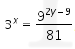 , maka nilai
, maka nilai ![]() adalah …..
adalah …..
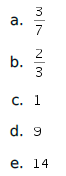
Pembahasan:
Perhatikan bahwa kita punya
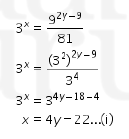 |
|
| dan | |
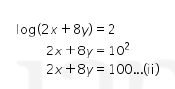 |
Kemudian, substitusikan (i) ke (ii) sehingga kita dapatkan
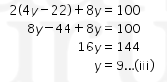 |
|
| Sehingga | |
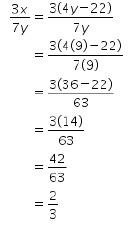 |
Jadi, jawaban yang tepat adalah B.

2.Rata-rata penjualan kaos (dalam kodi) selama 6 hari ditambah penjualan kaos hari ketujuh, nilainya empat kali rata-rata penjualan 6 hari. Jika jumlah penjualan hari ketujuh adalah 22 kodi, maka rata-rata penjualan selama 6 hari adalah … buah.
- 60
- 40
- 20
- 2
- 1
Pembahasan:
Misalkan ![]() adalah waktu penjualan pertama 6 hari,
adalah waktu penjualan pertama 6 hari, ![]() adalah waktu penjualan pertama ditambah hari ketujuh yaitu 7 hari,
adalah waktu penjualan pertama ditambah hari ketujuh yaitu 7 hari, ![]() adalah rata-rata penjualan 6 hari, dan
adalah rata-rata penjualan 6 hari, dan ![]() adalah rata-rata penjualan selama 7 hari, maka kita punya
adalah rata-rata penjualan selama 7 hari, maka kita punya
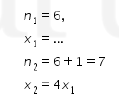
Perhatikan bahwa jumlah penjualan selama 7 hari sama dengan jumlah penjualan selama 6 hari ditambah penjualan hari ketujuh sehingga kita dapatkan
|
1 kodi = 20 buah, dengan demikian |
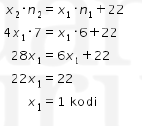
|
Maka rata-rata penjualan selama 6 hari adalah 20 buah.
Jadi, jawaban yang tepat adalah C.

| 3. |
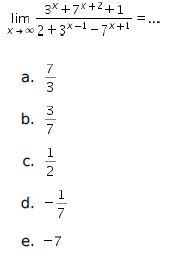 |
Pembahasan:
Perhatikan bahwa
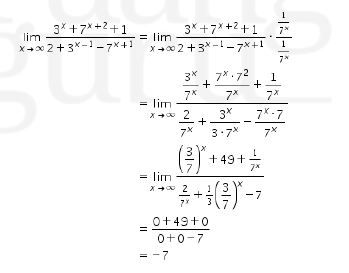
Jadi, jawaban yang tepat adalah E.

4. Sebuah tali dipotongmenjadi lima bagian dan membentuk deret aritmatika. Jika panjang tali terpendek adalah empat cm dan panjang tali semula adalah dua ratus cm, maka panjang tali yang ketiga adalah … cm.
- 9
- 10
- 19
- 20
- 40
Pembahasan:
Diketahui sebuah tali sepanjang 200 cm dipotong menjadi lima bagian dan membentuk deret aritmatika, maka kita punya
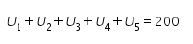 Ingat bahwa pada barisan aritmatika berlaku
Ingat bahwa pada barisan aritmatika berlaku
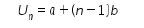 dengan a adalah suku pertama yaitu 4 dan b adalah beda, maka kita dapatkan
dengan a adalah suku pertama yaitu 4 dan b adalah beda, maka kita dapatkan
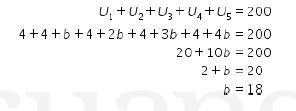 Sehingga
Sehingga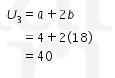
Maka panjang tali yang ketiga adalah 40 cm.
Jadi, jawaban yang tepat adalah E.

5. Diketahui (x, y) adalah penyelesaian dari sistem persamaan
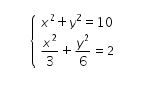
Jumlah dari semua nilai x yang memenuhi adalah …..
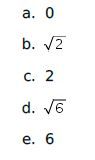
Pembahasan:
Diketahui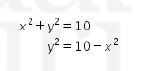 dan
dan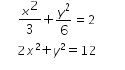
Maka, kita dapatkan
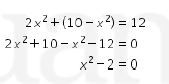
Degan menggunakan rumus jumlah akar-akar pada persamaan kuadrat di atas dengan a=1, b=0, c=-2, kita dapatkan
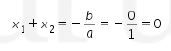
Maka, jumlah dari semua nilai x yang memenuhi adalah 0.
Jadi, jawaban yang tepat adalah A.

6. Diketahui persamaan kuadrat mempunyai akar-akar real p dan q. Jika p> -2 dan q> -2, maka nilai m adalah …..
- m> 8
- m> -8
- -8<m<8
- m<8
- m<-8
Pembahasan:
Perhatikan bahwa pada persamaan kuadrat 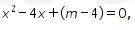 , didapatkan nilai a=1, b=-4 dan c=m-4.
, didapatkan nilai a=1, b=-4 dan c=m-4.
Karena akar-akarnya adalah p dan q, maka didapat hubungan
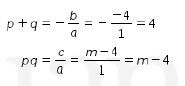
Karena persamaan kuadrat ini memiliki akar-akar real p dan q, maka haruslah D≥0. Dengan demikian, didapat
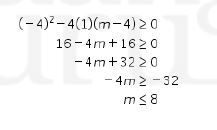
Karena p >-2 dan q>-2,maka didapat p+2 >0. Oleh karena itu, didapat

Karena m≤8dan m>-8, maka didapat -8<m≤8.
Jadi, jawaban yang tepat adalah C.

7. Nilai dari adalah a 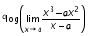 adalah …..
adalah …..
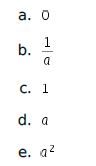
Pembahasan:
Ingat bahwa 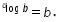
Oleh karena itu, didapat
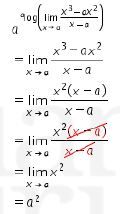
Jadi, jawaban yang tepat adalah E.

8. Jika 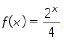 , maka
, maka 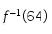 =
=
- 2
- 4
- 6
- 8
- 10
Pembahasan:
Misalkan 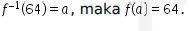
Karena 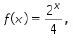 maka
maka
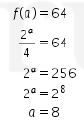
Dengan demikian, 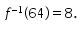
Jadi, jawaban yang tepat adalah D.

9. Perhatikan diagram berikut ini!
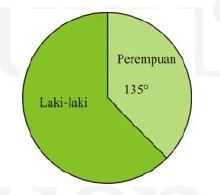
Diagram diatas menunjukkan diagram lingkaran dari peserta yang menghadiri sebuah pameran bayi. Di antara peserta laki-laki, didapatkan sebagai berikut.
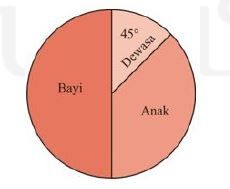
Jika dipilih satu orang secara acak, peluang terpilih seorang anak laki-laki adalah …..
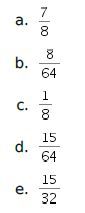
Pembahasan:
Misalkan L menyatakan kejadian terpilih seorang laki-laki dan A menyatakan kejadian terpilih seorang anak.
Dari diagram yang diberikan pada soal, didapat bahwa
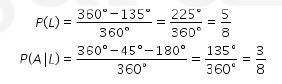
Peluang terpilih seorang anak laki-laki dapat dinyatakan sebagai berikut.
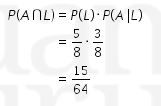
Jadi, jawaban yang tepat adalah D.

10. Diberikan kubus ABCD.EFGH dengan rusuk 8 cm. Jika P, Q, R, dan S berturut-turut adalah titik tengah AB, BC, GH, dan HE, maka jarak PQ ke RS adalah … cm.
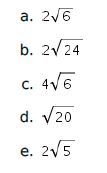
Pembahasan:
Perhatikan gambar berikut!
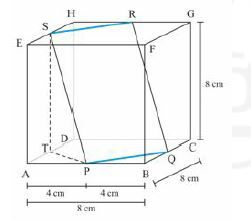
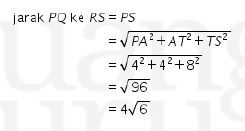
Maka, jarak PQ ke RS adalah 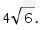
Jadi, jawaban yang tepat adalah C.

11. Diketahui bahwa 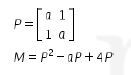
Jika 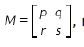 , maka nilai qr-ps adalah …..
, maka nilai qr-ps adalah …..
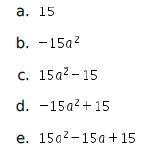
Pembahasan:
Diketahui bahwa
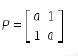
maka
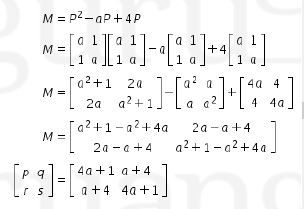
Jadi
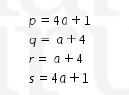
Sehingga didapat
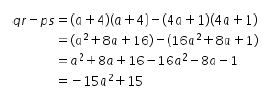
Dengan demikian,jawaban yang tepat adalah D.

12.Sebuah bengkel melayani jasa semir ban motor atau mobil dengan biaya Rp 6.000,00/ban. Jika tempat tersebut dapat menampung maksimal 40 kendaraan dan 92 ban, maka penghasilan maksimum yang dapat diperoleh bengkel tersebut adalah …..
- Rp 186.000,00
- Rp 240.000,00
- Rp 276.000,00
- Rp 290.000,00
- Rp 300.000,00
Pembahasan:
Misal banyaknya motor x unit dan banyaknya mobil y unit, maka pertidaksamaan yang sesuai dengan permasalahan diatas adalah sebagai berikut.
x+y < 40
2x+y < 92
x < 0
y < 0
Perhatikan terlebih dahulu garis x+y=40 dan 2x+4y=94.
Kemudian, cari titik potong dua garis.
Dari garis x+y=40, didapat x= -y+40.
Substitusikan x= -y+40 ke dalam 2x+4y=92, menjadi
2(-y+40)+4y=92
-2y+80+4y=92
2y=12
y=6
Substitusi y=6 ke x= -y+40, menjadi
x= -6+40
x+34
Jadi, titik potong kedua garis tersebut adalah (34,6).
Jika kedua pertidaksamaan awal digambarkan, maka menjadi
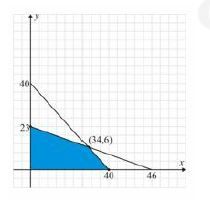
Dari gambar diatas didapat 4 titik pojok yang dilalui daerah arsiran (biru).
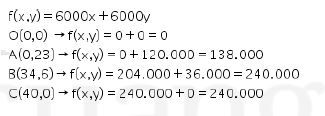
Jadi, penghasilan maksimum yang dapat diperoleh bengkel tersebut adalah Rp 240.000,00.
Dengan demikian,jawaban yang tepat adalah B.

13. D1 adalah daerah penyelesaian dari 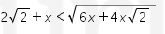
D2 adalah daerah penyelesaian dari 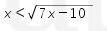
Maka pernyataan berikut yang paling tepat untuk D1 dan D2 adalah …..
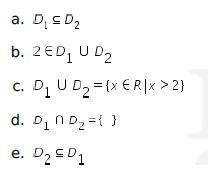
Pembahasan:
Perhatikan 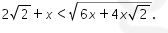
Pada bentuk 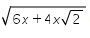 didapatkan syarat bahwa
didapatkan syarat bahwa
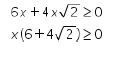
Karena 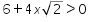 maka x> 0.
maka x> 0.
Akibatnya 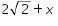 juga bernilai positif.
juga bernilai positif.
Karena 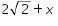 dan
dan 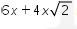 sama-sama bernilai positif, maka
sama-sama bernilai positif, maka
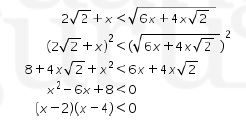
Sehingga
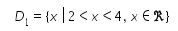
Selanjutnya perhatikan 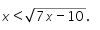
Pada bentuk 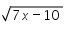 didapat syarat bahwa
didapat syarat bahwa
Karena 7x-10> 0 maka x> 0.
Akibatnya x juga bernilai positif.
Karena x dan 7x-10 sama-sama bernilai positif, maka
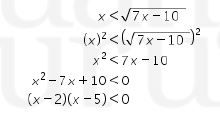
Sehingga
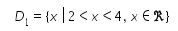
Dapat dilihat bahwa 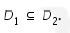
Jadi, pernyataan yang tepat adalah 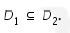
Dengan demikian,jawaban yang tepat adalah A.

14. Diketahui 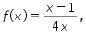 g(x)=2z-3, dan h(x) adalah fungsi yang memenuhi (g o h) (x) = 2x+5. Bentuk sederhana dari
g(x)=2z-3, dan h(x) adalah fungsi yang memenuhi (g o h) (x) = 2x+5. Bentuk sederhana dari 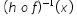 adalah …..
adalah …..
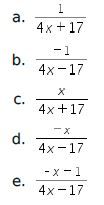
Pembahasan:
Perhatikan bahwa
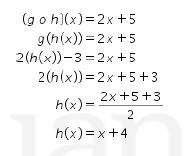
Sehingga
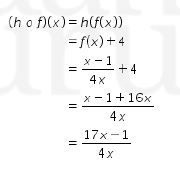
Kemudian mencari invers dari (h o f) (x)
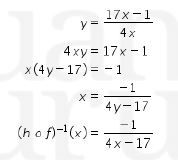
Jadi, bentuk sederhana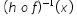 dari adalah
dari adalah 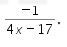
Dengan demikian,jawaban yang tepat adalah B.

15. Diberikan fungsi f dan g yang mempunyai invers. Jika f(g(x))=4x+3 dan g(x+1)= x-2 maka nilai 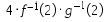 adalah …..
adalah …..
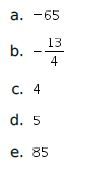
Pembahasan
Perhatikan bahwa
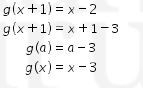
Sehingga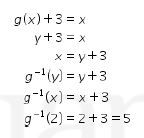
Selanjutnya, perhatikan bahwa
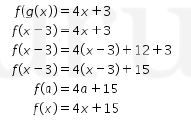
Sehingga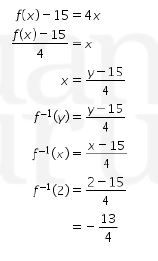
Maka, kita dapatkan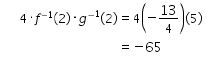
Jadi, jawaban yang tepat adalah A.

16. Diketahui rumus ketinggian adalah 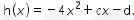 Jika grafik memotong sumbu x di titik (-2, 0) dan (4, 0), maka hmax dari grafik tersebut adalah …..
Jika grafik memotong sumbu x di titik (-2, 0) dan (4, 0), maka hmax dari grafik tersebut adalah …..
- -4
- 0
- 1
- 36
- 44
Pembahasan:
Diketahui
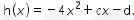 dengan a= -4, memotong titik (-2, 0) dan (4, 0).
dengan a= -4, memotong titik (-2, 0) dan (4, 0).
maka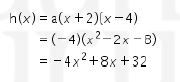
Kemudian, menentukkan tmax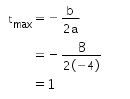 Selanjutnya, mencari
Selanjutnya, mencari 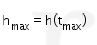
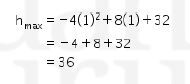 Jadi,hmax =36
Jadi,hmax =36
Dengan demikian,jawaban yang tepat adalah D.

17. Diketahui
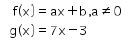
Jika f(x) merupakan invers dari g(x), maka nilai dari adalah …..
Pembahasan:
Dari soal diketahui bahwa
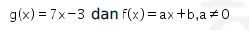
serta f(x) merupakan invers dari g(x),
pertama kita tentukan invers dari g(x) terlebih dahulu
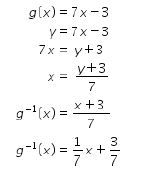
Karena f(x) merupakan g(x) maka
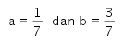
Sehingga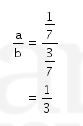
Jadi, nilai dari 
Jadi, jawaban yang tepat adalah B.

18. Diketahui
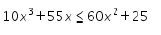
Maka nilai x yang memenuhi adalah …..
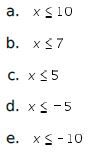
Pembahasan:
Untuk menentukan nilai x yang memenuhi, perhatikan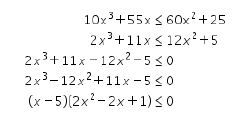 Kemudian, tentukan nilai diskriminan dari
Kemudian, tentukan nilai diskriminan dari 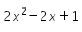 , didapat
, didapat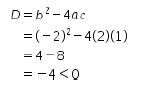 dan
dan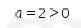
Oleh karena itu 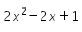 , disebut definit positif, akibatnya
, disebut definit positif, akibatnya
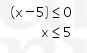 Jadi, nilai x yang memenuhi adalah
Jadi, nilai x yang memenuhi adalah ![]() .
.
Dengan demikian,jawaban yang tepat adalah C.

19. Jika diketahui xn adalah suku ke-n dari suatu barisan aritmatika xk+4= xk+p dengan p≠0 yang untuk sembarang bilangan asli positif k, maka x6+x10+x14+…+x4n+2 adalah …..
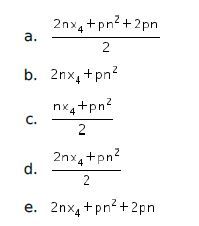
Pembahasan:
Perhatikan bahwa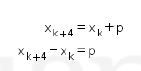
Perhatikan pula bahwa xn adalah suku ke-n dari suatu barisan aritmatika. Misalkan suku pertama dari barisan aritmatika tersebut adalah a dan bedanya adalah b, maka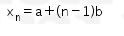 Oleh karena itu,
Oleh karena itu,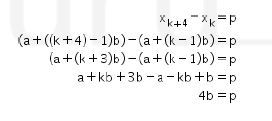 Perhatikan deret x6+x10+x14+…+x4n+2
Perhatikan deret x6+x10+x14+…+x4n+2
Suku pertama dari deret tersebut adalah x6 dan bedanya adalah 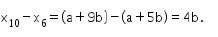
Perhatikan bahwa Jadi, x4n+2 adalah suku ke-n dari deret tersebut.
Jadi, x4n+2 adalah suku ke-n dari deret tersebut.
Oleh karena itu, deret x6+x10+x14+…+x4n+2 memiliki n suku.
Dengan demikian, didapat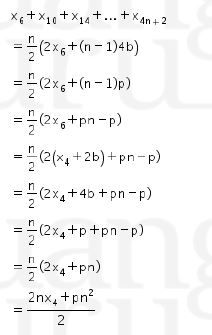 Jadi, jawaban yang tepat adalah D.
Jadi, jawaban yang tepat adalah D.

20. Diketahui FX=EFX, dimana FX merupakan ordo 2 x 2.
Jika 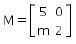 dan L= EM, maka L-1 adalah …..
dan L= EM, maka L-1 adalah …..
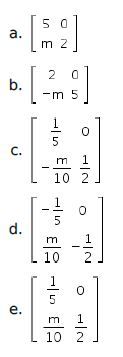
Pembahasan:
Dari,
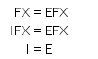
Didapatkan bahwa E adalah matriks Indentitas
Sehingga
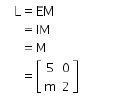
Invers matriks L
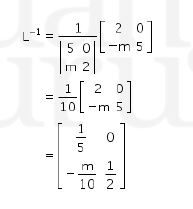 Maka L-1 adalah
Maka L-1 adalah 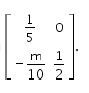
Jadi, jawaban yang tepat adalah C.

Pelaksanaan UTBK memang masih tahun depan, tapi nggak ada salahnya untuk kamu mulai mempersiapkan diri mulai sekarang. Mau mengukur kemampuanmu dalam mengerjakan soal-soal UTBK? Tunggu tryout UTBK Episode 2 dari ruanguji!