Pembahasan Soal TVRI 30 Juli 2020 Kelas 4-6 SD, SMP, dan SMA

Artikel ini memberikan pembahasan soal tayangan TVRI tanggal 30 Juli 2020 untuk kelas 4-6 SD, SMP, dan SMA
—
Hai, sudah pada nonton program Belajar dari Rumah yang ditayangkan di TVRI hari ini tanggal 30 Juli 2020 belum? Pada tayangan hari ini, siswa SD kelas 4-6 belajar mengenai Faktor dan Kelipatan, siswa SMP belajar tentang Pola Bilangan, dan siswa SMA belajar mengenai Persamaan Eksponen Bentuk 4, 5, dan 6. Nah, buat kamu yang sudah belajar, dan pengen tahu pembahasan soal dari tayangan TVRI hari ini, yuk pelajari di artikel ini.

1. Tim tari Ekskul SD Makmur terdiri dari 8 orang. Tim tari akan mengikuti Lomba Porseni. Tiap tim menampilkan berbagai bentuk formasi tarian. Berapa formasi tarian yang dapat dibentuk oleh tim tari tersebut?
Jawaban:
Untuk menentukan banyak formasi tarian yang mungkin dari 8 orang, kita cari faktor dari 8 seperti pada tabel berikut.

Dari sini kita peroleh kemungkinan formasi yang dapat dibentuk oleh tim tari tersebut adalah formasi 18 atau 24. Jadi, banyak formasi tarian yang dapat dibentuk adalah 2 formasi.

2. Sepasang bilangan prima antara 15 dan 30 jumlahnya 52 dan bedanya 6. Pasangan bilangan prima manakah itu?
JAWABAN
Perhatikan ya.. bilangan prima yang ada di antara 15 dan 30 adalah 17, 19, 23, dan 29.
Sekarang kita cari sepasang bilangan dari 17, 19, 23, dan 29 yang jumlahnya adalah 52 dan beda atau selisihnya adalah 6.
Kita coba satu persatu ya.
Jika bilangan yang pertama adalah 17, maka 17 ditambah bilangan kedua harus sama dengan 52, sehingga bilangan keduanya adalah 52 – 17 = 35. Karena 35 bukan bilangan prima dan tidak berada di antara 15 dan 30, maka bilangan prima yang dimaksud bukan 17.
Berikutnya, jika bilangan yang pertama adalah 19, maka 19 ditambah bilangan kedua harus sama dengan 52, sehingga bilangan keduanya adalah 52 – 19 = 33. Karena 33 bukan bilangan prima dan tidak berada di antara 15 dan 30, maka bilangan prima yang dimaksud bukan 19.
Selanjutnya, jika bilangan prima yang pertama adalah 23, maka 23 ditambah bilangan kedua harus sama dengan 52, sehingga bilangan keduanya adalah 52 – 23 = 29. Waaah perhatikan bahwa 29 adalah bilangan prima di antara 15 dan 30 nih. Sekarang kita periksa bedanya yaa. Bedanya adalah 29 – 23 = 6.
Jadi, sepasang bilangan prima tersebut adalah 23 dan 29, karena jumlahnya adalah 52 dan bedanya 6.

3. Leni, Siti, dan Dina bermain lompat tali di halaman depan rumahnya. Mereka bermain secara bergantian sesuai dengan urutan masing-masing. Leni mendapat urutan ketiga. Jika Leni bermain sebanyak 8 kali, pada urutan ke berapa Leni bermain lagi?
JAWABAN
Kelipatan dari 3 adalah: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, dan seterusnya.
Karena Leni bermain sebanyak 8 kali, setelah bermain pada urutan ke-3, maka Leni akan bermain lagi pada urutan ke- 6, 9, 12, 15, 18, 21, dan 24.

1. Perhatikan susunan bilangan berikut. (i) 3, 8, 13, 15, 18, 27 (ii) 4, 7, 10, 13, 16, 19 (iii) 5, 9, 13, 18, 24, 27 (iv) 6, 9, 12, 15, 17, 20 Ani berpendapat yang merupakan barisan bilangan adalah (i) dan (ii) Budi berpendapat yang merupakan barisan bilangan adalah (i) dan (iii) Cepi berpendapat yang merupakan barisan bilangan adalah (ii) dan (iii) Dadan berpendapat yang merupakan barisan bilangan adalah (ii) dan (iv) Menurut kamu, pendapat siapa yang tepat? Jelaskan alasanmu!
Jawaban:
Ingat kembali yaa barisan bilangan adalah susunan bilangan yang memiliki pola atau aturan tertentu antara satu bilangan dengan bilangan berikutnya.
Nah untuk tahu yang mana merupakan barisan bilangan, kita amati pola setiap barisan di atas.
(i) Perhatikan untuk pola 3, 8, 13, 15, 18, 27 berikut ini!
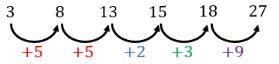
Karena pola bilangan ketiga dan setusnya berbeda, maka barisan 3, 8, 13, 15, 18, 27 bukan barisan bilangan.
(ii) Perhatikan untuk pola 4, 7, 10, 13, 16, 19 berikut ini!
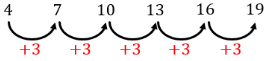
Karena pola bilangan di atas selalu sama antara satu bilangan dengan bilangan berikutnya, yaitu selalu bertambah 3, maka barisan 3, 8, 13, 15, 18, 27 merupakan barisan bilangan.
(iii) Perhatikan untuk pola 5, 9, 13, 18, 24, 27 berikut ini!
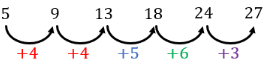
Karena pola bilangan ketiga dan setusnya berbeda, maka barisan 5, 9, 13, 18, 24, 27 bukan barisan bilangan.
(iv) Perhatikan untuk pola 6, 9, 12, 15, 17, 20 berikut ini!
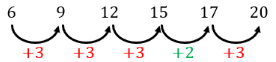
Karena pola bilangan ketiga dan setusnya berbeda, maka barisan 6, 9, 12, 15, 17, 20 bukan barisan bilangan.
Sehingga barisan yang merupakan barisan bilangan hanya barisan nomor (ii). Akibatnya tidak ada pendapat yang benar mengenai barisan ini.

2. Perhatikan pola susunan batang korek api berikut!

Pola 1 Pola 2 Pola 3 Pola 4 Rendi berpendapat bahwa jumlah minimal batang korek api untuk membuat pola yang ke-10 adalah 33 buah. Menurut kamu, apakah pendapat Rendi tepat?Jelaskan alasanmu!
Jawaban:
Perhatikan jumlah batang korek api disetiap polanya!
Pola 1 terdiri dari 6 batang korek api
Pola 2 terdiri dari 9 batang korek api
Pola 3 terdiri dari 12 batang korek api
Pola 4 terdiri dari 15 batang korek api
Kemudian jika kita amati penambahan jumlah batang korek api disetiap polanya yaitu :
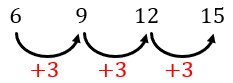
Nah, ternyata penambahan banyak batang korek api antara satu pola dengan pola berikutnya selalu sama, yaitu bertambah 3. Perhatikan operasi hitung pada setiap pola :
Pola 1→6 = 3⋅1 + 3
Pola 2→9 = 3⋅2 + 3
Pola 3→12 = 3⋅3 + 3
Pola 4→15 = 3⋅4 + 3
…
Pola n→…= 3⋅n + 3
Sehingga pola ke-10 dapat diperoleh dengan mengganti n = 10. Maka,
Pola 10 = 3⋅10 + 3 = 30 + 3 = 33
Diperoleh banyak batang korek api pada pola kesepuluh adalah 33.
Jadi, pendapat Rendi benar.

3. Perhatikan pola susunan batang korek api berikut!
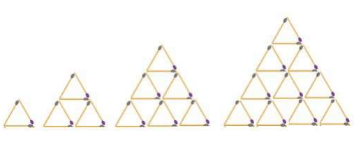
Dimas berpendapat bahwa jumlah minimal batang korek api untuk membuat pola yang ke-7 adalah 60 buah. Menurut kamu apakah pendapat Dimas tepat? Jelaskan alasanmu!
Jawaban:
Perhatikan jumlah batang korek api disetiap polanya!
Pola 1 terdiri dari 1 segitiga atau 3 batang korek api
Pola 2 terdiri dari 3 segitiga atau 9 batang korek api
Pola 3 terdiri dari 6 segitiga atau 18 batang korek api
Pola 4 terdiri dari 10 segitiga atau 30 batang korek api
Terlihat bahwa untuk pola ke-n maka banyak batang korek api dapat dihitung dari banyak segitiga yang terbentuk dikalikan dengan 3. Nah, untuk mendapat banyak korek api pada pola ke-7, kita cari dulu banyak segitiga di pola ke-7 tersebut.
Perhatikan pola berikut!
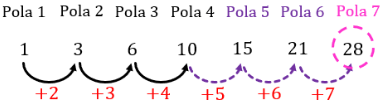
Maka pada pola ke-7 akan ada 28 bentuk segitiga. Sehingga jumlah minimal batang korek api pada pola ke-7 adalah 28×3 = 84 buah.
Jadi, pendapat Dimas salah.

1. Apakah solusi dari persamaan (2x + 1) 3x-6 = (x+3) 3x-6, hanya x = 2? Jelaskan jawabanmu!
Jawaban:
Dari soal, diberikan persamaan eksponensial sebagai berikut.
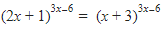
Nah, ini kan bentuknya 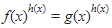 . berarti, ada tiga kemungkinan dari sini
. berarti, ada tiga kemungkinan dari sini
- f (x) = g (x),
- h (x) = 0, dengan syarat f(x)≠0, g(x)≠0, dan
- fx = – g(x), dengan syarat h(x) bilangan genap.
Yang artinya kemungkinan-kemungkinan ini harus dicek satu per satu biar dapet solusi-solusinya.
1. Misalkan f (x) = g (x). Artinya adalah
2x+1 = x+32x-x = 3-1x = 2
Kita dapet satu hasil, yaitu x = 2. Nah ini nih yang dibilang di soal, bahwa salah satu solusinya itu adalah x = 2. Apakah masih ada lagi kemungkinan solusinya? Mari kita lanjutkan
2. Misalkan h (x) = 0, dengan f (x) ≠ 0 dan g (x) ≠0. Nah sebentar, sebelumnya lihat dulu f(x)≠0. Dari sini, didapat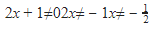
Terus, lihat juga g(x)≠0. Dari sini, sama, didapat
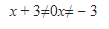 Oke, sekarang kita dapat syarat
Oke, sekarang kita dapat syarat 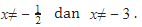 Karena udah kita tetapkan demikian, baru kita masuk ke hx=0. Didapat
Karena udah kita tetapkan demikian, baru kita masuk ke hx=0. Didapat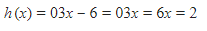
Oke, lagi-lagi didapat x=2 sebagai solusi. Apakah ada lagi solusi lain? Kita lihat syarat terakhir.
3. Misalkan fx=-g(x) dengan h(x) adalah bilangan genap. Nah, lagi-lagi, lihat deh syarat hx adalah bilangan genap ini.
Coba diingat, bilangan genap itu apa? Bilangan genap itu ya ±2, ±4, ±6, ±8, ±10, dst begitu ya? Jadi, hasil yang kita dapat harus membuat si h(x) ini menjadi bilangan genap.
Oke, kita coba ya. Dari fx=-g(x), maka
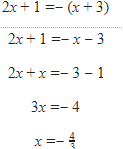
Nah udah dapet hasil nih, yaitu 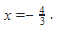 Kita tes, substitusikan ke h(x), jadinya bilangan genap atau bukan.
Kita tes, substitusikan ke h(x), jadinya bilangan genap atau bukan.
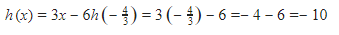
Wah, 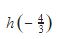 jadi bilangan genap ya, yaitu -10. Walaupun negatif, tetapi -10 adalah bilangan genap. Karena apa? Karena dia habis dibagi oleh 2.
jadi bilangan genap ya, yaitu -10. Walaupun negatif, tetapi -10 adalah bilangan genap. Karena apa? Karena dia habis dibagi oleh 2.
Jadi didapat satu solusi lagi (selain x=2) yaitu 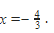 Kalau mau dites apakah solusi yang kita dapatkan sudah benar, tinggal substitusikan ke persamaan pada soal itu.
Kalau mau dites apakah solusi yang kita dapatkan sudah benar, tinggal substitusikan ke persamaan pada soal itu.
Misalkan x=2, maka
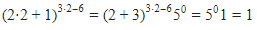
Hasilnya bernilai benar. Berarti x=2 salah satu solusinya.
Kemudian, misalkan 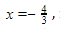 maka
maka
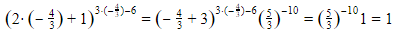
Hasilnya bernilai benar, berarti 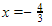 salah satu solusinya.
salah satu solusinya.
Berarti, solusinya tidak hanya x=2, tetapi juga 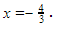

2. Tentukan himpunan penyelesaian dari persamaan (x + 1)3x+6 = (x2 + 2x + 1)2x+5
Jawaban:
Dari soal, diberikan persamaan eksponensial sebagai berikut.
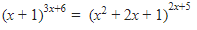
Nah, ini kan bentuknya 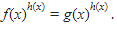 Eh tapi, sebentar. Coba dilihat deh. Perhatikan bahwa
Eh tapi, sebentar. Coba dilihat deh. Perhatikan bahwa
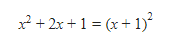
Berarti
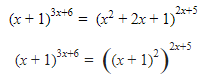
Ingat kembali bahwa 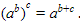 Jadinya seperti ini nih.
Jadinya seperti ini nih.
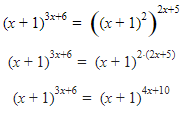
Nah, ternyata bentuknya adalah 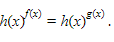 Jadi, dari sini didapat beberapa kemungkinan
Jadi, dari sini didapat beberapa kemungkinan

Jadi sekarang akan diperiksa masing-masing kemungkinannya.

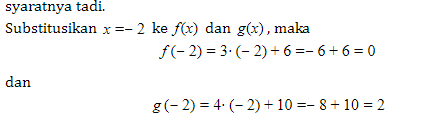
Nah sekarang kita lihat nih. Ada 0 dan 2. Apakah keduanya bilangan ganjil? Bukan ya, karena 0 dan 2 bukan bilangan ganjil. Berarti, bilangan genap? Iya! Betul. Kesimpulannya adalah x = -2 juga solusi. Jika disubstitusikan x=-2 ke persamaan pada soal, maka
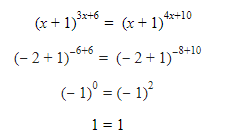
Yang menghasilkan pernyataan yang bernilai benar.
Jadi, solusi dari persamaan pada soal adalah x = -4, x = 0, x = -1, dan x = -2. Kalau dibuat sebagai himpunan penyelesaian, maka 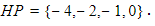

3. Hitunglah jumlah akar-akar persamaan 4x + 1 – 12 (2x) + 8 = 0
Jawaban:
Dari soal, diberikan persamaan eksponensial sebagai berikut.
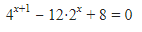
Nah, coba temen-temen pehatikan deh. Bentuk ini bisa disederhanakan menjadi seperti ini
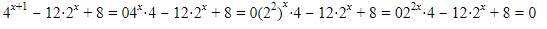
Oke. Ada banyak bentuk 2x nih. Dimisalkan aja jika 2x=y, berarti (2x)2=y2 dan 22x=y2. Maka didapat
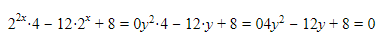
Wah jadi persamaan kuadrat ya. Berarti bisa difaktorkan menjadi
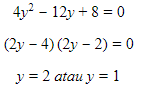
Nah dapet nih, dua buah akar. Yaitu y=2 dan y=1. Ingat kembali bahwa tadi kita memisalkan y=2x. Sekarang kita substitusikan balik nih, jadi
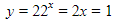
dan
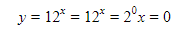
Oke deh, jadi didapat dua buah solusi, yaitu x = 0 dan x = 1. Jika dijumlahkan, maka hasilnya adalah 0 + 1 = 1.
Sehingga jumlah akar-akarnya (atau solusi-solusinya) adalah 1.

Gimana? Jelas dan mudah dipahami kan pembahasannya? Ohya, jangan lupa untuk terus update pembahasan soal latihan TVRI di ruangbaca setiap harinya ya. Kamu juga bisa lho mengerjakan latihan soal lainnya di ruangbelajar.














