Bentuk-Bentuk Persamaan Logaritma dan Cara Menyelesaikannya | Matematika Kelas 10

Bentuk-bentuk persamaan logaritma ada apa aja, ya? Terus, gimana cara menyelesaikannya? Yuk, simak penjelasannya dalam artikel berikut!
—
Kalian pasti udah tau dong, kalo gempa itu adalah gelombang atau getaran yang merambat dan aktivitasnya bisa direkam pakai seismograf? Nah, tapi kamu tau nggak sih, gimana caranya seseorang menentukan intensitas gempa?
Jadi, intensitas gempa itu bisa diukur dengan skala richter. Skala ini menggunakan prinsip dari logaritma dengan basis 10.
Sebenarnya, masih banyak sih, contoh penerapan prinsip logaritma yang lainnya, misalnya taraf intensitas bunyi, mengukur pH atau tingkat asam suatu zat, dan lain sebagainya.
Nah, pas banget nih, sama materi yang bakal kita bahas kali ini, yaitu persamaan logaritma.
Untuk materi logaritmanya sendiri, mungkin rata-rata dari kalian belum pernah belajar ya, waktu di SMP dulu. Tapi, walaupun materi ini baru kalian temuin di SMA, materinya seru dan nggak susah kok!
Sebelum kita ke pembahasan persamaan logaritma, make sure kamu harus udah paham konsep awal logaritma. Tapi, kalo kamu masih belum jelas, coba kamu check artikel tersebut, ya.
Oke, kalo gitu langsung aja kita mulai pembahasan persamaan logaritma!
Pengertian Persamaan Logaritma
Persamaan logaritma adalah persamaan yang memuat bentuk logaritma dengan basis atau numerus, atau keduanya memuat variabel. Jadi maksudnya, ada dua bentuk logaritma (di ruas kiri dan kanan) dimana basis atau numerus atau keduanya memuat variabel, kemudian kedua ruas ini dihubungan dengan tanda sama dengan. Nilai x yang memenuhi persamaan ini disebut dengan penyelesaian dari persamaan tersebut.
Sebelumnya, masih inget kan sama bentuk umum logaritma yang ini:
alog x = n
a = basis atau bilangan pokok, dengan syarat a > 0 dan a≠1
x = numerus, dengan syarat x > 0
n = nilai logaritma
Terus, kalau persamaan logaritma bentuknya gimana ya?
Bentuknya sama seperti bentuk umum logaritma, tapi pada persamaan logaritma, bentuk logaritmanya ada dua di ruas kiri dan kanan lalu dihubungkan menggunakan tanda sama dengan. Contohnya seperti ini, nih:
3log (2x+9) = 3log (10x – 16)
Nanti kita akan bahas lebih lanjut ya, gimana caranya untuk mendapatkan nilai x yang memenuhi persamaan tersebut. Tapi sebelum itu, kita bahas bentuk-bentuk persamaan logaritma dulu, ya!
Bentuk-Bentuk Persamaan Logaritma
Nggak jauh beda dari materi eksponen, persamaan logaritma juga punya beberapa bentuk yang bikin kamu lebih gampang untuk mengidentifikasi nilai peubahnya. Nah, ini dia bentuk-bentuk persamaan logaritma:

Wah, keliatannya ribet ya. Tapi padahal nggak sesusah itu kok. Sederhananya, logaritma memiliki enam bentuk seperti yang bisa kamu lihat pada gambar di atas.
Bentuk Pertama
Sekarang kita coba bahas mulai dari bentuk yang pertama, yaitu alog f(x) = alog n. Coba perhatikan gambar berikut!

Nah, supaya kamu lebih paham, kita langsung masuk ke contoh soal ya, sekalian kita belajar gimana cara menyelesaikan persamaannya.
Contoh soal:
Tentukan nilai x yang memenuhi persamaan logaritma berikut ini:
- 3log (3x+6) = 3log 9
- 2log (x+9) = 5
Jawab:
a. 3log (3x+6) = 3log 9
Karena basis dari logaritmanya nilainya sama, maka nilai numerusnya juga akan sama. Sehingga bisa kita tulis seperti berikut:
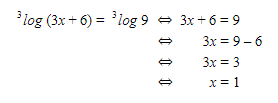
Kemudian, kita bisa uji numerus, jadi kita substitusi x = 1 ke 3x + 6.
3x + 6 = 3(1) + 6 = 9
Nah, ketemu nih, hasilnya adalah 9, di mana 9 > 0, maka syarat numerus f(x) > 0 terpenuhi. Jadi, penyelesaian 3log (3x+6) = 3log 9 adalah x = 1.
b. 2log (x+9) = 5
Nah, untuk menyelesaikan persamaan ini, kita ubah ruas kanan ke bentuk logaritma terlebih dahulu, dengan memilih nilai basis yang sama dengan ruas kiri, dan memanfaatkan sifat alog bc = c alog b. Maka menjadi seperti berikut:
2log (x+9) = 5 x 2log 2
2log (x+9) = 2log 25 (5 kita pindah sebagai pangkat dan ini nggak mengubah nilai, hanya mengubah bentuknya aja)
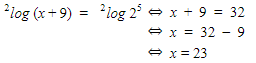
Lanjut, kita uji numerus, (x+9) = 23 + 9 = 32, karena 32 > 0, maka syarat terpenuhi. Jadi, nilai x yang memenuhi persamaan 2log (x+9) = 5 adalah 23.
Sekarang kita lanjut ke bentuk persamaan logaritma yang kedua, yuk!
Bentuk Kedua
Bentuk persamaan logaritma yang kedua, hampir sama dengan bentuk yang pertama tadi, tapi numerusnya berbeda.

Kita langsung kerjakan contoh soal, ya!
Contoh soal:
Tentukan nilai x yang memenuhi persamaan log (x2 – 2x – 15) = log (x + 3)!
Jawab:
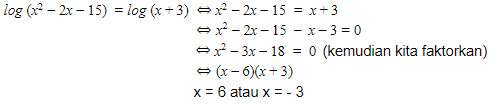
Nah, sampai disini kita bisa uji syarat numerus.
- Untuk x = – 3
f(x) = x2 – 2x -15 = (-3)2 – 2(- 3) -15 = 0
g(x) = x2 + 3 = (-3)2+3 = 12
Walau g(x) > 0 tapi f(x) = 0, jadi x = -3 tidak memenuhi persamaan logaritma ini. Lanjut untuk x = 6.
- Untuk x = 6
f(x) = x2-2x-15 = (6)2-2(6)-15 = 9
g(x) = x2+3= (6)2+3 = 39
Memenuhi karena f(x) dan g(x) > 0.
Jadi, nilai x yang memenuhi persamaan log (x2-2x-15) = log (x+3) adalah x = 6.
Sekarang, lanjut ke bentuk ketiga!
Bentuk Ketiga
Untuk bentuk persamaan logaritma yang ketiga, bentuknya adalah seperti infografik di bawah ini. Coba perhatikan!

Di persamaan ketiga ini numerusnya sama, tapi basisnya berbeda.
Contoh soal:
Tentukan nilai x yang memenuhi persamaan 2log (5x-9) = 5log (5x-9)!
Jawab:
Karena numerus sama yaitu 5x – 9 dan kedua basis nilainya lebih dari 0, berarti sudah dipastikan numerus = 1.
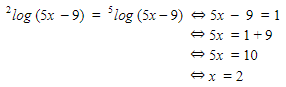
Kita bisa melakukan uji numerus, 5x – 9 = 5(2) – 9 = 1 di mana 1 > 0 dan syarat terpenuhi. Penyelesaian dari 2log(5x-9) = 5log(5x-9) persamaan adalah x = 2. Gimana seru kann? yuk kita bahas bentuk selanjutnya!
Bentuk Keempat
Oke guys, kita udah sampai di bentuk persamaan logaritma yang keempat. Perhatikan infografik di bawah.

Persamaan ini hampir mirip kayak bentuk persamaan nomor 2. Bedanya, basis sama numerus punya variabel, tapi basis di kiri dan kanan tetap sama ya, kaya gini nih!
Contoh soal:
Tentukan nilai x yang memenuhi persamaan x-1log (x2-16) = x-1log (5x-2)!
Jawab:
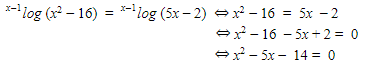
kemudian kita faktorkan (x – 7) ( x + 2) diperoleh x = 7 dan x = -2
Lalu kita uji syarat basis dan numerusnya, agar lebih mudah kita pakai tabel aja ya.
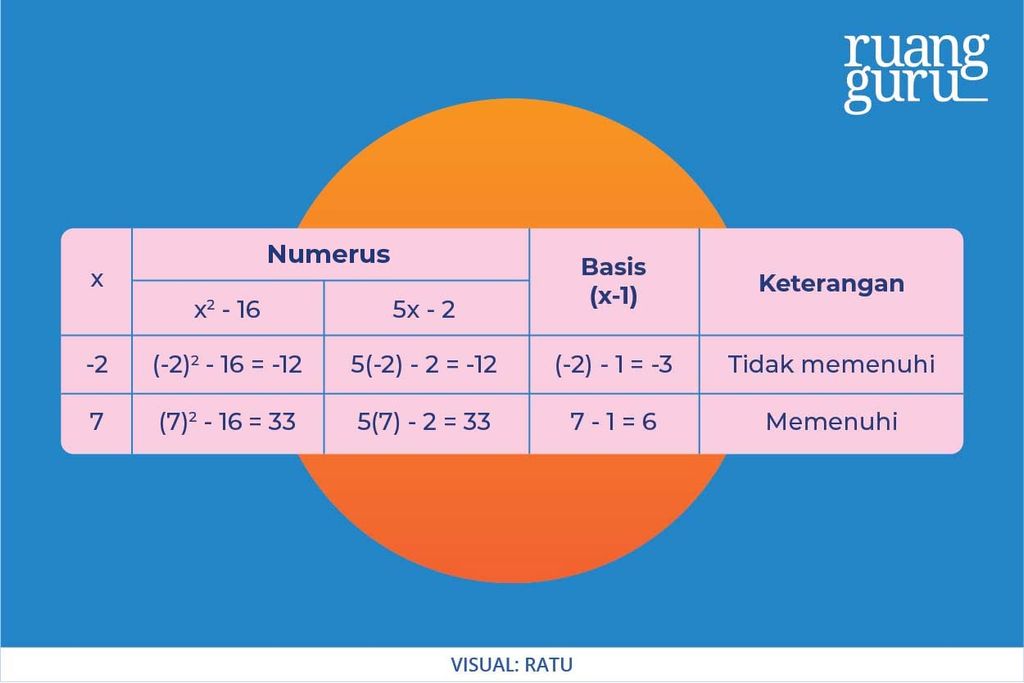
Karena x = 7 menghasilkan numerus x2 – 7 dan 5x -2 yang lebih dari 0, kemudian basis x-1 yang lebih dari 0 dan tidak sama dengan 1, maka hanya x = 7 yang memenuhi syarat logaritmanya. Jadi, penyelesaian dari persamaan ini adalah x = 7.
Bentuk Kelima
Nah, untuk bentuk kelima, kamu bisa perhatikan infografik berikut. Jangan lupa perhatikan syaratnya juga, ya!

Untuk bentuk kelima ini, tipenya seperti bentuk yang sebelumnya (memiliki variabel di numerus dan basis), tapi basis di kiri dan kanan berbeda.
Contoh soal:
Tentukan penyelesaian persamaan x+3log (x2-5) = 2x-1log (x2-5)!
Jawab:
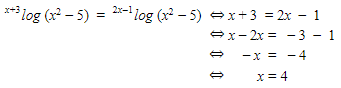
Lanjut kita uji syarat basis dan numerusnya, ya!
- Uji Basis
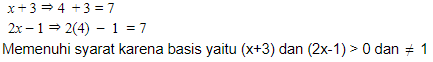
- Uji Numerus
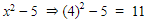
Memenuhi syarat karena numerus > 0 - Saat x2 – 5 = 1, maka x = ±√6
Tapi, yang memenuhi hanya √6 saja karena hanya nilai √6 yang memenuhi syarat basis dan numerus.
Oke, kita udah dapet nih, penyelesaian persamaan x+3log (x2-5) = 2x-1log (x2-5) yaitu x = 4.
Bentuk Keenam
Bentuk keenam atau bentuk terakhir ini agak berbeda dari persamaan sebelumnya ya, karena bentuk persamaan logaritma ini membentuk persamaan kuadrat. Perhatikan infografik berikut ini ya:

Supaya kamu bisa nyelesain persamaan yang dikasih, tugas kamu harus memisalkan logaritma jadi bentuk. Nah, dari permisalan itu, kamu bakal dapet bentuk persamaan kuadratnya.
Contoh soal:
Tentukan penyelesaian persamaan 3log2 x – 3log x3 – 4 = 0!
Jawab:
Walau dari bentuk umum tandanya plus, tapi kita bisa menjumpai soal yang tandanya minus seperti halnya persamaan kuadrat,
3log2 x – 3log x3 – 4 = 0 bisa juga ditulis dengan 3log2 x+ (-3log x3) + (-4)
Jadi, gak ada masalah ya untuk tanda plus dan minus, yang penting kamu fokus di basis dan numerusnya.
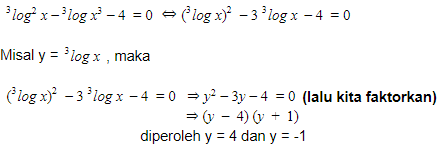
Oke, supaya kita dapet nilai x-nya, langsung aja kita substitusi nilai y ke permisalan.
- Untuk y = 4
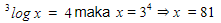
- Untuk y = -1
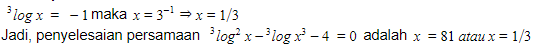
Wahhh, akhirnya selesai juga nih bahasan kita tentang bentuk-bentuk persamaan logaritma dan cara menyelesaikannya. Sekarang kamu udah lebih ngerti, kan? Intinya, kamu harus mengingat syarat-syarat dari masing-masing bentuk. Jangan sampai tertukar!
Oh ya, setelah baca ini jangan langsung bobo yaa hehehe, karena kamu harus banget latihan soal di ruangbelajar. Pemahaman kamu tentang persamaan logaritma ini bakal lebih keren lagi deh, karena fitur di ruangbelajar lengkap banget, mulai dari latihan soal yang selalu update dan juga pembahasan yang asik plus mudah dimengerti dari Master Teacher. So, tunggu apalagi? Yuk, ke ruangbelajar!
Referensi:
Sinaga, B. (2014). Matematika SMA/MA Kelas X Semester 1. Jakarta: Pusat Perbukuan, Departemen Pendidikan Nasional.
Artikel ini telah diperbarui pada 28 September 2021.












